Věda a technika v pozadí
Závod z kopečka
Teorie
Nejedná se totiž o volný pád. Všechna tři tělesa totiž nekonají posuvný pohyb, ale pohyb otáčivý. Zatímco u posuvného pohybu se pohybují všechny body tělesa stejnou rychlostí, u pohybu otáčivého záleží jejich rychlost na vzdálenosti od středu otáčení.
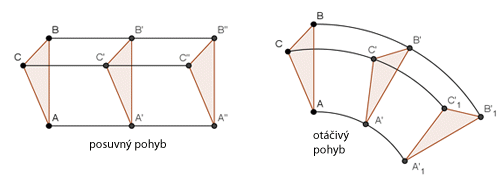
Posuvný a otáčivý pohyb.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Důležitým rozdílem všech tří valících se těles je rozložení jejich hmoty v tělese. Díky tomu má každé těleso jiný moment setrvačnosti. Tak jako potřebujeme více energie, abychom dali do pohybu hmotnější těleso, potřebujeme více energie, abychom dali do rotačního pohybu těleso s větším momentem setrvačnosti. Máme-li dvě kola o stejné hmotnosti, mají stejnou setrvačnost, pokud vykonávají pouze posuvný pohyb. Nemají však stejný moment setrvačnosti, neboť ten je závislý na rozložení hmotnosti kola. Pro kolo, které má svoji hmotnost rozloženou po obvodu kola, je těžší dostat se do rotace než pro kolo, které má svoji hmotnost rozloženou rovnoměrně nebo u středu. Proto se bude prstenec otáčet pomaleji než disk.
Při otáčivém pohybu tuhého tělesa kolem nehybné osy opisují body tělesa kružnice, jejichž středy leží na ose otáčení. Úhlová rychlost w pohybu je pro všechny body tělesa stejná, velikosti rychlostí jednotlivých bodů jsou přímo úměrné jejich vzdálenosti od osy otáčení. Moment setrvačnosti vzhledem k ose otáčení se označuje písmenem J, jednotkou momentu setrvačnosti je kg m2. Moment setrvačnosti závisí na rozměrech a tvaru tělesa a na poloze osy otáčení vzhledem k tělesu. Nejsnadněji lze vypočítat moment setrvačnosti stejnorodých souměrných těles vzhledem k ose otáčení procházející těžištěm.
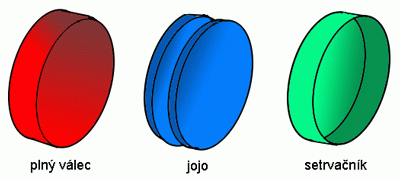
Tvary těles z exponátu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Hmotnost všech tří těles v exponátu je přibližně stejná. Valivý odpor je u tak malých těles a rychlostí zanedbatelný. Rozhoduje tedy moment setrvačnosti. Pod kopec přijede nejdříve kolo s nejmenším momentem setrvačnosti (jojo) a nakonec s největším momentem setrvačnosti (setrvačník).
Setrvačník nebo také gyroskop je zařízení o velké hmotnosti, které se otáčí velkou rychlostí kolem osy souměrnosti. Ty jsou navrhovány tak, aby rotovaly kolem své volné osy. Osa roztočeného setrvačníku zachovává svůj směr v prostoru, nepůsobí–li na setrvačník vnější síly. Ke změně směru rotační osy je třeba poměrně velkého momentu síly. Roztočený setrvačník má značnou kinetickou energii. Těžké setrvačníky u parních motorů vyrovnávají náhlá zatížení nebo odlehčení strojů, takže chod je rovnoměrnější, mimoto dodávají energii v taktech, kdy stroj práci nekoná.
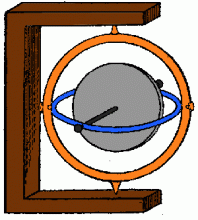
Setrvačník v Cardanově závěsu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Roztočením si setrvačník nastřádá velmi mnoho energie a dlouho se pak točí. Je–li moment vnějších sil působících na setrvačník roven nule, nemění osa otáčení svůj směr. Příkladem je setrvačník zavěšený v Cardanově závěsu, který se skládá ze dvou na sebe kolmých kruhů. Těleso zavěšené v tomto závěsu nemění osu otáčení, i když měníme polohu celého setrvačníku.
Setrvačníky mají řadu praktických použití. Jako bezmomentový setrvačník uložený v Cardanově závěsu se chová umělý horizont, zařízení, které umožňuje pilotům určit horizontální polohu. Setrvačníky umožňují stabilizovat kmity lodi při silném vlnobití. Pět setrvačníků pomáhá zajišťovat stabilitu vozítka segway.


