Věda a technika v pozadí Kulečník

Celkový přehled Veřejnost MŠ 1. stupeň ZŠ 2. stupeň ZŠ SŠ VŠ

Jak exponát vypadá

Jak exponát vypadá:

Autor textu

Autor textu:

Mgr. Magda Králová

Exponát má na starosti

Exponát má na starosti:

Mgr. Kristýna Nová

O čem je tento exponát

O čem je tento exponát:

V Techmanii si můžete vyzkoušet eliptický kulečníkový stůl. Objevte, jak je v něm možné, že se koule snadno dostane jakýmkoli šťouchem z vyznačeného bodu do díry!

Kulečník v dnešní podobě se hraje už nejméně osm století. Pochází z Anglie, kde se pomocí zahnutých holí posouvaly po trávníku koule skrz branku, za níž byla koule, do které se hráči museli trefit, a tato druhá koule pak měla porazit kuželku. Odtud také pochází název hry – billy (koule) a yard (dvůr, hřiště). S modernizací se pak pokračovalo ve Francii. V současnosti patří mezi kulečníhové hry karambol (stůl bez děr, tři koule), pool (stůl se šesti děrami v rozích, s rozdílným počtem koulí), snooker a ruský kulečník (stůl s děrami v desce, ne v rozích).

Teorie

Apollónios z Pergy je autorem osmisvazkového díla Kuželosečky. První čtyři knihy se dochovaly v řečtině, další tři v arabském překladu a poslední se ztratila. Apollóniův přístup ke kuželosečkám se neobvykle velkou všeobecností odlišuje od metod všech jeho předchůdců. Zatímco do Apollónia se každý z třech druhů kuželoseček získával z různých druhů kruhových kuželů, Apollónius je všechny získával z libovolného kruhového kuželu bez ohledu na to, či je přímý nebo kosý. Jako první zavedl dodnes používané pojmenování pro kuželosečky: elipsa, parabola a hyperbola. Apollóniova metoda předstihla metodu analytické geometrie. Objevují se v ní první náznaky souřadnicového systému.

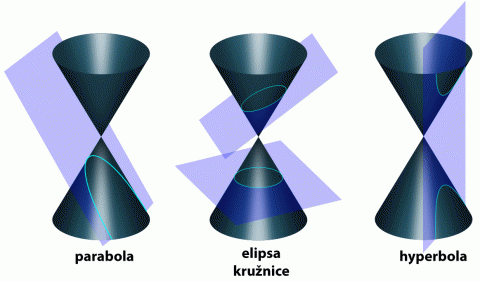
Všechny známé kuželosečky můžeme vyrobit řezáním kuželu. Představte si dva kužele spojené ve vrcholu, které jsou nekonečné. Jestliže budeme kužel řezat rovinou kolmou na osu kužele, dostaneme kružnici. Když tuto rovinu trošku nakloníme, řezem bude elipsa. Při dalším naklánění roviny se nám řez náhle "otevře", dostali jsme parabolu. Stačí jen malé vychýlení roviny a řez bude dvojdílný, protože rovina v této poloze protne oba dva kužele. Řezem je tentokrát hyperbola.

Vznik kuželoseček řezem kuželu.
Zdroj: commons.wikimedia.org. Under Creative Commons.

Podívejme se podrobně na elipsu. Elipsa je množina všech bodů roviny, které mají od dvou navzájem různých pevných bodů E, F konstantní součet vzdáleností 2a, přičemž platí: 0 < |EF| < 2e < 2a. Tato písmena označují základní charakteristiky elipsy: a hlavní poloosa elipsy, b vedlejší poloosa elipsy, e excentricita elipsy e² = a² - b², S střed elipsy, A, B hlavní vrcholy elipsy, C, D vedlejší vrcholy elipsy, E, F ohniska elipsy.

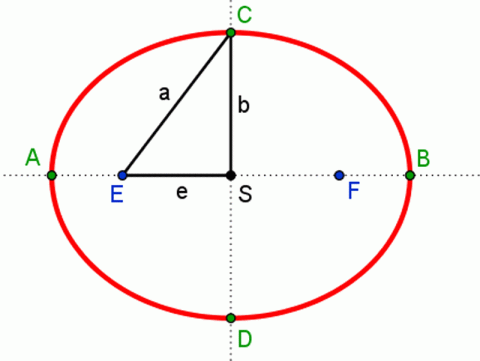
Základní charakteristiky elipsy.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.

S elipsou se setkáme v nebeské mechanice jako trajektorie dvojhvězd, dráhy planet apod. Elipsu lze zkonstruovat pomocí zahradnické metody. Do země zapíchneme dva kolíky, které představují ohniska elipsy (tj. jejich vzdálenost je 2e). Na kolíky připevníme špagát délky 2a a vezmeme třetí kolík, pomocí kterého napneme špagát a pohybujeme jím: všechny místa, které kolíkem na zemi označíme, jsou body elipsy. Na stejném principu jako tato konstrukce funguje i šťouchání koulí na speciálním kulečníkovém stole v exponátu.