Věda a technika v pozadí
Setrvačník
Teorie
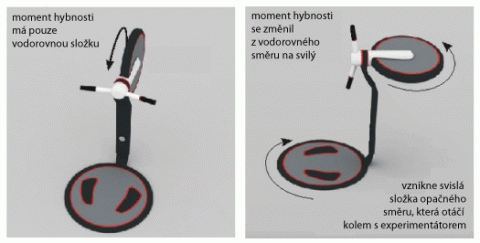
Funkce setrvačníku je založena na zákonu zachování momentu hybnosti izolované soustavy. Pokud nepůsobí na soustavu momenty vnějších sil, moment hybnosti soustavy se zachovává ve všech složkách. Izolovaná soustava je právě taková, kde nepůsobí žádné momenty vnějších sil. Máme-li tedy na počátku roztočené kolo ve svislé poloze, má moment hybnosti pouze vodorovnou složku a svislá složka je nulová.
Princip exponátu Setrvačník.
Zdroj: Techmania Science Center. Under Creative Commons.
Po otočení rotujícího kola se směr momentu hybnosti změní na svislý. Musí tedy existovat jiná svislá složka momentu hybnosti mířící na druhou stranu tak, aby se momenty vykompenzovaly a svislá složka byla stále nulová. Jedině pak bude splněn zákon zachování momentu hybnosti. Druhou složku svislého momentu hybnosti tvoří právě stolička spolu s experimentátorem, která rotuje na druhou stranu než kolo, a tím kompenzuje svislou složku.
Chceme-li odvodit vztah pro úhlovou rychlost rotace plošinky, musíme vyjít ze vztahu pro moment hybnosti. Ten určíme zvlášť pro rotující kolo a zvlášť pro plošinku, na které stojí experimentátor.
Úhlové rychlosti obou rotujících plošinek.
Zdroj: Techmania Science Center. Under Creative Commons.
Pro moment hybnosti L vzhledem k pevné ose platí
kde J je moment setrvačnosti a ω je úhlová rychlost. Máme-li rotující tuhé těleso, závisí jeho moment setrvačnosti na rozložení hmoty v tomto tělese. V případě různých těles o stejné hmotnosti bude největší moment setrvačnosti u tělesa, jehož hmota je umístěna dále od osy otáčení. Obecně moment setrvačnosti závisí na hmotnosti a druhé mocnině vzdálenosti od osy otáčení. Pokud bychom nahradili experimentátora o hmotnosti M plným válcem o poloměru R, pak můžeme vztah pro moment hybnosti experimentátora přepsat
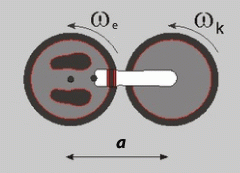
Plošinka a kolo nejsou souosé, vzdálenost obou os je a. Musíme proto moment setrvačnosti kola odvodit pomocí Steinerovy věty. Pro moment hybnosti pak můžeme psát
kde m je hmotnost kola a r jeho poloměr. Na začátku pohybu byla vodorovná složka momentu hybnosti nulová, musí být tedy nulová i po otočení kola. Pro součet obou momentů hybnosti proto musí platit
a po dosazení
Můžeme vyjádřit úhlovou rychlost plošinky s experimentátorem
Záporné znaménko značí, že se plošinka s experimentátorem otáčí opačným směrem než kolo. Úhlová rychlost experimentátora závisí na vzdálenosti osy kola od osy plošinky. Čím bude tato vzdálenost větší, tím pomaleji se bude experimentátor pohybovat. Takto vypočítaná úhlová rychlost experimentátora je pouze přibližná, hlavně kvůli přibližnému určení momentu setrvačnosti experimentátora. Přesto lze říct, že rychlost rotace experimentátora závisí na tom, jak rychle se podaří roztočit kolo a hlavně na hmotnosti experimentátora.
Setrvačník nebo také gyroskop je zařízení o velké hmotnosti, které se otáčí velkou rychlostí kolem osy souměrnosti. Ty jsou navrhovány tak, aby rotovaly kolem své volné osy. Osa roztočeného setrvačníku zachovává svůj směr v prostoru, nepůsobí–li na setrvačník vnější síly. Ke změně směru rotační osy je třeba poměrně velkého momentu síly. Roztočený setrvačník má značnou kinetickou energii. Těžké setrvačníky u parních motorů vyrovnávají náhlá zatížení nebo odlehčení strojů, takže chod je rovnoměrnější, mimoto dodávají energii v taktech, kdy stroj práci nekoná.
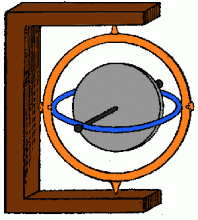
Setrvačník v Cardanově závěsu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.Roztočením si setrvačník nastřádá velmi mnoho energie a dlouho se pak točí. Je–li moment vnějších sil působících na setrvačník roven nule, nemění osa otáčení svůj směr. Příkladem je setrvačník zavěšený v Cardanově závěsu, který se skládá ze dvou na sebe kolmých kruhů. Těleso zavěšené v tomto závěsu nemění osu otáčení, i když měníme polohu celého setrvačníku.
Setrvačníky mají řadu praktických použití. Jako bezmomentový setrvačník uložený v Cardanově závěsu se chová umělý horizont, zařízení, které umožňuje pilotům určit horizontální polohu. Setrvačníky umožňují stabilizovat kmity lodi při silném vlnobití. Pět setrvačníků pomáhá zajišťovat stabilitu vozítka segway.
