Věda a technika v pozadí
Pythagorova věta
Historie
Věta pojmenovaná po řeckém matematikovi Pythagorovi byla formulovaná již dříve Babyloňany a Číňany. Na babylonských hliněných tabulkách z 18. století před n. l se objevil součet 32 + 42 = 52. Používal se k vytyčování oltářů. Pythagoras nebo někdo z jeho školy zveřejnil první důkaz věty.
Pythagoras.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Teorie
Pythagorova věta popisuje vztah mezi délkami stran libovolného pravoúhlého trojúhelníku v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Věta zní:
Součet obsahů čtverců nad oběma odvěsnami se rovná obsahu čtverce nad přeponou.
Formálně Pythagorovu větu vyjadřuje rovnice
kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou označeny a, b.
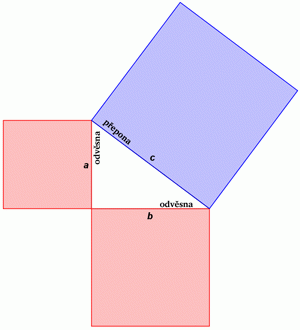
Pravoúhlý trojúhelník.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Pythagorovu větu zná téměř každý, její důkaz zvládne málokdo, i když jich existuje cca 400. Jeden z nich vymyslel i bývalý americký prezident J. A. Garfield. Kromě exponátu v Techmanii nás o její platnosti přesvědčí třeba tento jednoduchý důkaz.
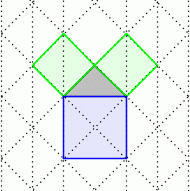
Jeden z důkazů pythagorovy věty.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Čtverce v Pythagorově větě můžeme nahradit i jinými plošnými obrazci (půlkružnicí, obdélníkem, trojúhelníkem, pětiúhelníkem) za předpokladu, že jsou si navzájem podobné a jejich strana je shodná s délkou příslušné strany trojúhelníku. Součet obsahů těchto obrazců nad odvěsnami bude opět shodný s obsahem obrazce nad přeponou.
Pythagorovu větu můžeme zobecnit pro obecný trojúhelník do tvaru tzv. kosinové věty
kde a, b, c jsou strany trojúhelníku.
Pythagorejská čísla jsou taková tři kladná čísla, že součet čtverců dvou z nich dává čtverec třetího čísla. Jsou to například čísla 3, 4, 5 (32 + 42 = 52) nebo 5, 12, 13. Eukleides dokázal, že takových trojic kladných čísel je nekonečně mnoho. Můžeme je vyjádřit v obecném tvaru pomocí libovolných přirozených čísel
Pythagorejská čísla mají řadu aplikací. Pokud potřebujeme vytyčit v přírodě pravý úhel a nemáme k dispozici úhelník, tak použijeme pythagorejská čísla 3, 4, 5. Vzdálenost 3 a 4 naneseme na dvě ramena, která mají svírat pravý úhel a pak změříme úhlopříčku. Pokud není přesně 5, tak úhel není pravý.
